浙江海洋大学

波浪能作为新兴能源具有广阔的前景及市场，目前国内外已设计开发多种类型的波浪能装置，以促进波浪能的开发。其中，以英国海蛇为代表的筏式波浪能装置，由于结构简单，生存能力强，转换效率高等特点，在离岸式波浪发电装置中成为不错的选择。

为了提升筏式波浪能装置的工作效率，国内外众多学者展开了详细的研究，包括改变其结构尺寸、吃水、外形等，或者是增加额外的装置来提高其波浪能捕获效率，比如阻尼板、张力弹簧等。研究表明，通过优化铰接连接处的方式，能够更为明显地提高装置的纵摇运动的频率，以及拓宽其低频捕获频带。

对于铰接连接模式，浙江海洋大学船舶与海运学院徐鹏副教授与其研究生陈炫宇研究团队提出了一种创新的双铰接配置设计，旨在通过优化浮体间的连接模式，提高能量捕获效率并扩展低频捕获带宽。目前研究成果已在工程类传统国际顶级期刊《Energy》（中科院分区一区，TOP期刊）上发表。

一、研究方案

从改变铰接连接方式来提高筏式波浪能捕获效率的角度出发，以解决基于液压系统的筏式WEC在实际工程中故障率高且结构易受大载荷破坏以及在非线性波浪中装置发电效率低、适应性差、生存时间短等问题。

研究团队采用实验与数值模拟相结合的方法，系统评估了单铰接和双铰接配置对双筏式WEC性能的影响。为了更真实地了解WEC在海洋条件下的性能，进一步考察了装置在不规则波和不同波浪入射角下，两种铰接配置的WEC的能量捕获效率和铰接链接处的受力载荷。研究方案包括：

实验设计：构建了单铰接和双铰接双链接形式的双浮体物理模型，并在拖曳水池中进行实验，研究其六自由度运动响应与系泊张力的变化和规律。

数值模拟：结合实验数据，验证数值模型后，基于弱非线性三维势流软件AQWA对不同铰接配置下的双浮体的捕能特性进行多维度的数值模拟研究。

动作捕捉技术应用：利用青瞳视觉（CHINGMU）动作捕捉系统，实时监测浮体的纵摇响应、相对角速度及系泊张力等关键数据，为实验提供高精度的动态响应数据支持。

二、物理模型实验

（一）实验设置

实验在长度130米，宽度6米，最大水深4.0米的水槽中进行。为了减轻波浪反射的影响，在水槽的末端安装了波浪吸收系统，为实验提供一个受控且多功能的实验环境。

实验装置：

双筏式WEC模型：单铰接和双铰接配置，浮体间距可调。

动捕系统：由六个光学运动捕捉相机组成，采样频率120Hz，实时监测浮体的运动轨迹和姿态。

造波装置：液压摇摆板，可生成频率范围0.1Hz—2.0Hz的波浪。

双浮体模型的尺寸为1.2m长、0.6m宽和0.3m高。同时，为了与传统铰接形式做对比，实验模型考虑了单铰接形式的双浮体的运动响应。并采用了类似以往实验中采用简单线性阻尼模型的方法，将铰接器中的阻尼来表示PTO系统的抗转矩，如图1所示：

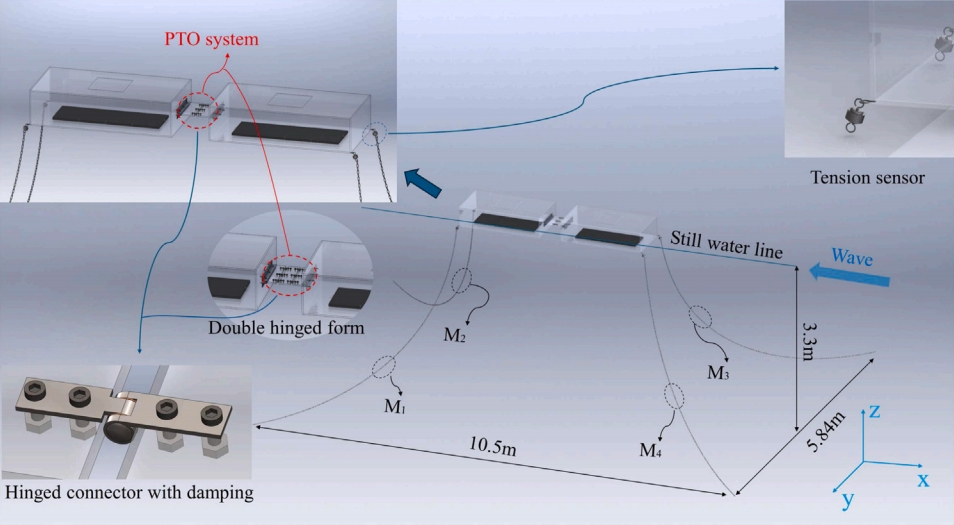
图1.WEC和系泊系统的示意图

实验使用监测设备来监测两个浮体之间的纵摇运动响应以及相对角速度，其中包含8个光学运动捕捉摄像机围绕粘贴了红外反光球的筏式WEC。此外，四根系泊分别配备了水下拉力传感器，通过数据采集器传输到电脑上后进行数据监测。如图2所示：

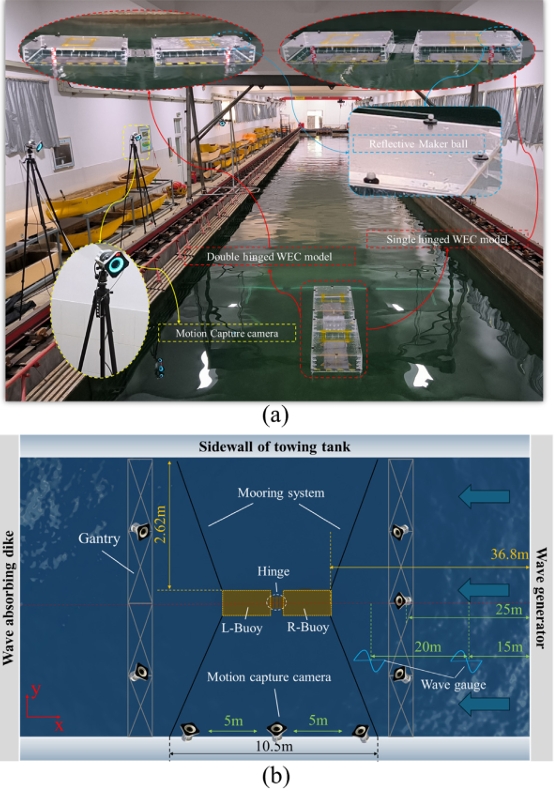
图2.模型实验中筏式WEC的实验装置： (a）标记有反光点的双浮体； （b）实验装置。

同时，为了保证数据的可靠性和科学性，实验中所使用的数据是双浮体运动稳定运行的十个波浪周期下的运动数据。并且，在完成一种波浪条件下的实验工况的数据采集后，待水面平静后才开始下一组实验测试。

此外，除了铰接方式，浮体间距也是影响双浮体连接的重要参数之一，为此，在模型实验中考虑了不同间距下双浮体的运动通过评估前后浮体之间的纵摇响应和角速度差异来确定两个浮体之间的相对纵摇角，确保了在实验框架内对目标运动和姿态进行精确且多维度的评估。如图3所示，其中d为双浮体的间距，L为浮体的特征长度。

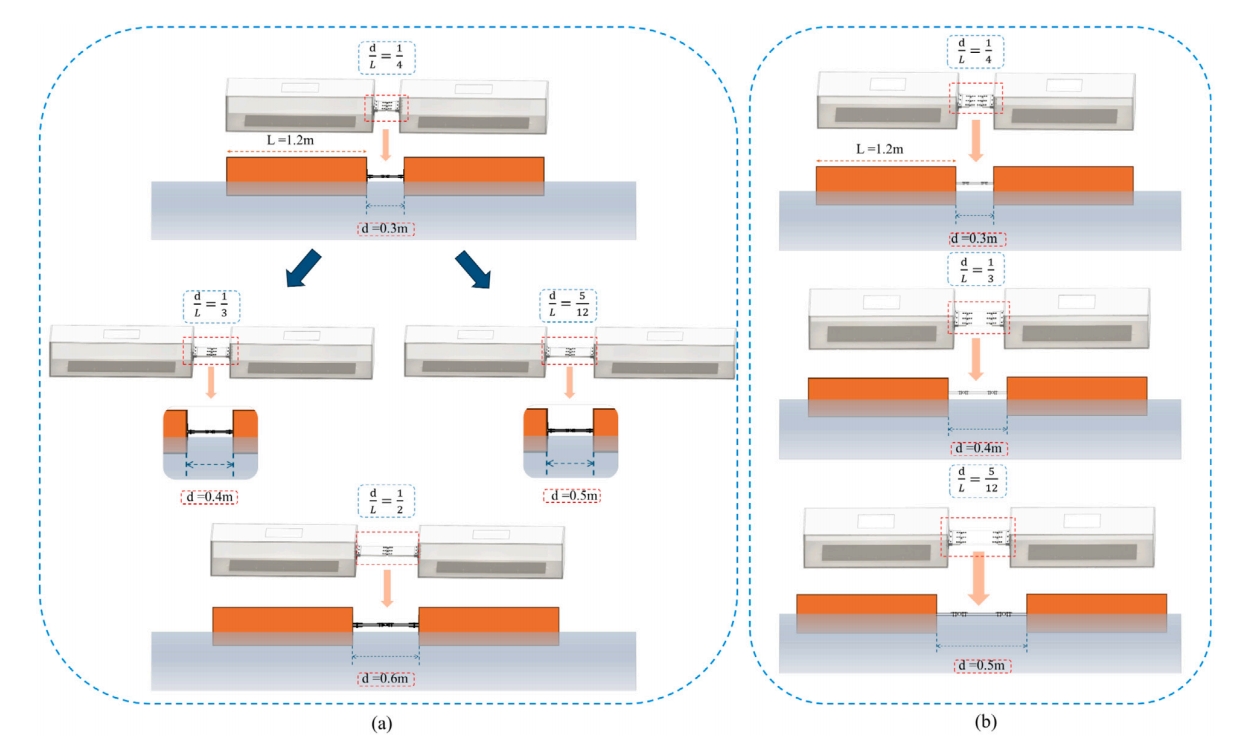
图3.基于不同d/L比的双桨型WEC状态： （a）单铰接式WEC模型; （b）双铰接式WEC模型。

为了避免出现严重的上浪现象，模型实验中研究了双铰接和单铰接双筏式WEC在波高为0.10米情况下的姿态性能。并且，将单铰接浮体的浮体间距条件设定为从0.30米（d∕L=1/4）开始，以避免浮体间距设置过短对双浮体的运动产生的不利影响。如表1所示：

表1：单个浮体模型的主要尺寸

实验结果表明，适当的浮体间距可以合理利用装置的水动力相互作用，提高双浮体的相对纵摇运动，从而提高能量捕获效率。这些发现强调了优化浮子间距以提高波浪能转换系统性能的重要性。

同时，实验也表明，筏式波浪能发电装置的能量捕获效率与波长有关。能量捕获宽度比最初会增加，然后随着波长的增加而减小。当λ/L约为2.0（相当于单个浮子的长度等于波长的一半）时，浮子的能量捕获效率最为明显，能量捕获效率最大化。受多种因素的影响，因此，最佳波频范围存在于最显著的中间值，从而获得最大俘能效率。为了优化筏式波浪能发电装置的尺寸，最好与当地海域的典型波长保持2:1的比例。与此同时，不同浮体间距也显著影响着双浮体的俘能效率。如图4所示：

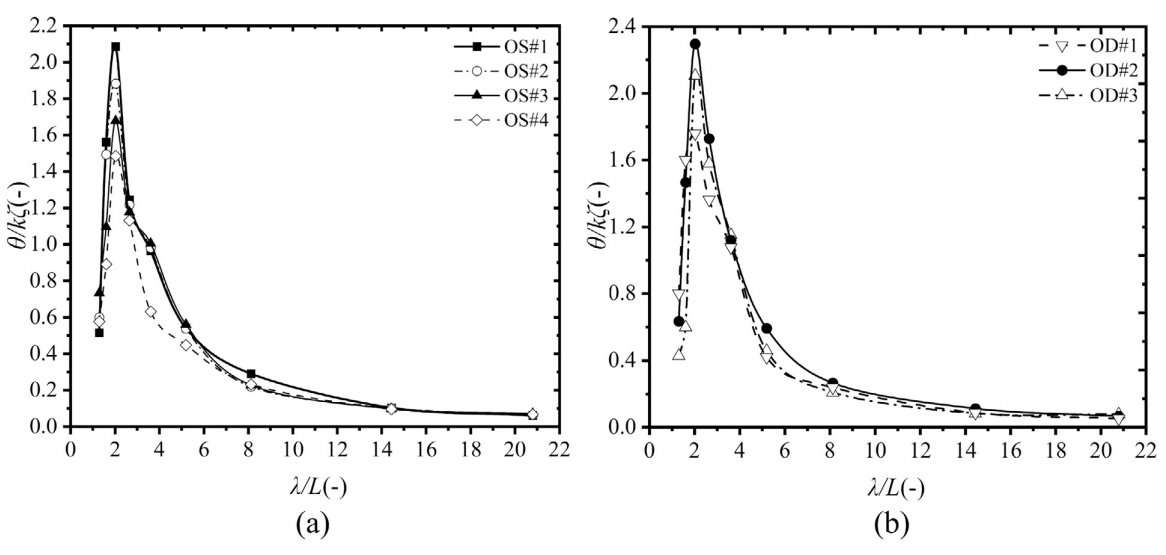
图4：各种铰接式WEC模型在不同d/L比下的相对螺距： （a）单铰接式WEC模型在不同d/L比下的比较 （b）双铰接式WEC模型在不同d/L比下的比较。

三、数值模型验证

（一）数值工具：

数值模拟部分更为详细地考虑了不同波浪参数下双铰接和单铰接筏式WEC在运动响应与捕获效率方面的差异。

为了确保稳健性和计算效率，该研究的数值模拟主要依赖于基于势流的软件进行模拟。同时，在初始水动力响应计算中，为了准确描绘两个相互连接的浮动体在波浪环境中的运动学特性，采用了多层级坐标系的方法。如图5所示：

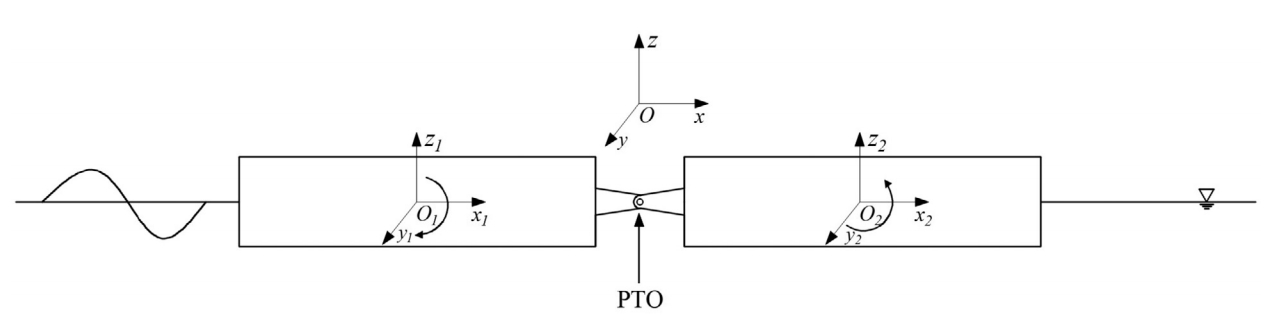
图5.使用坐标系描述筏式WEC在波浪中的运动

同时，后续俘能效率计算PTO(Power take-off,动力输出)单元以如图6和7表示，以阐明其功能作用。在筏式WEC中，PTO 系统位于两个筏之间，因此有必要将其表示为以旋转阻尼系数C为其特征的扭转阻尼器。这一理论结构基于PTO线性等效旋转理论。

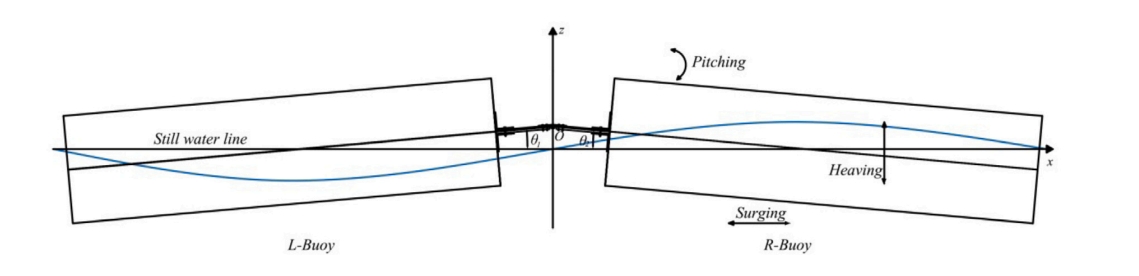
图6.筏式WEC的纵摇角示意图

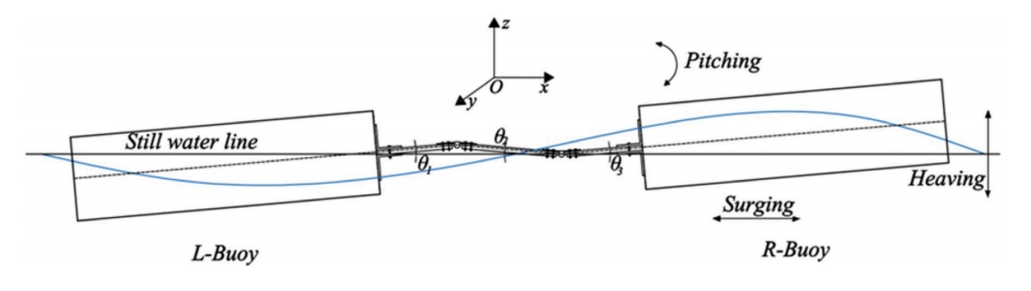
图7.双铰接式WEC的示意图，说明了旋转PT0系统

（二）数值模型验证：

从实验结果可知，双筏式WEC的主要纵摇响应频率区间在3.14 rad/s～5.65 rad/s 之间，为此，数值模拟重点验证这一区间内的双浮体相对纵摇运动。为了进一步验证数值模型的有效性。分别验证了单铰接和双铰接配置下WEC单个浮体的纵摇运动响应。对比显示，模拟结果与实验数据在纵摇动态响应方面表现出显著的一致性。为了提高这些求解器预测的精度，在PTO系统中设设置了合适的阻尼系数，以完善模拟结果。如图8、9、10所示：

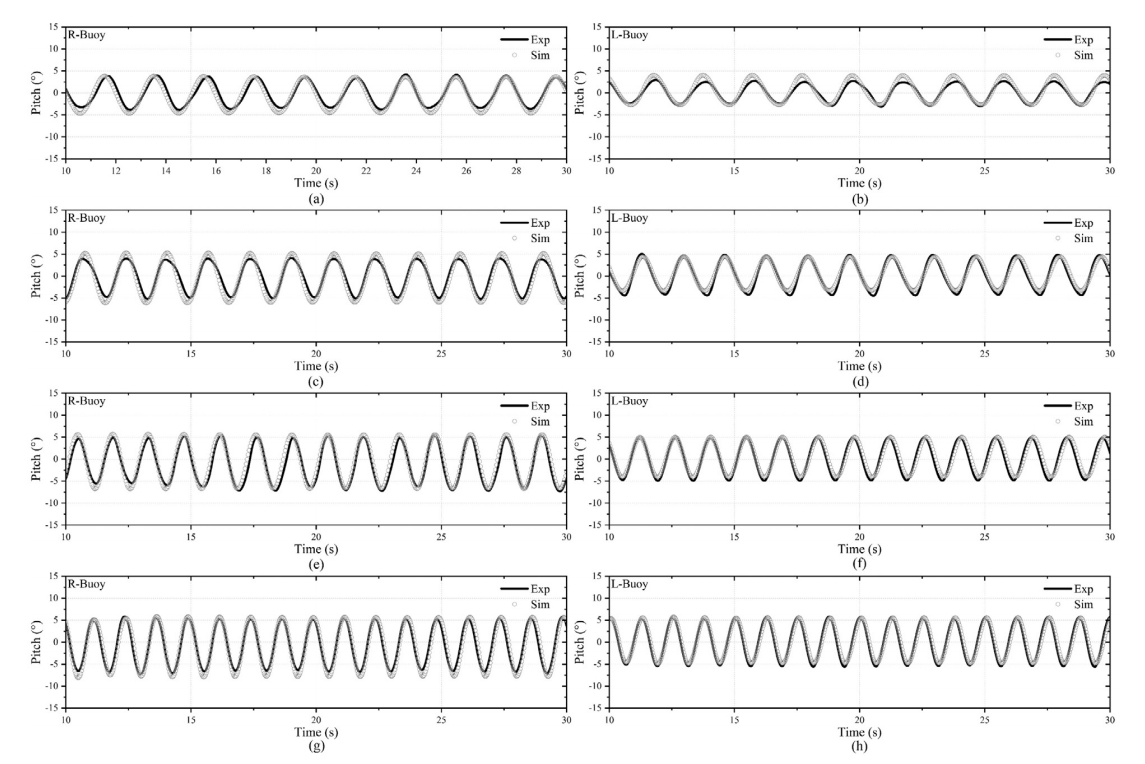
图8：单铰接式波浪能转换器（WEC）数值模拟与试验结果对比验证（d/L=1/4）：
(a) 右侧浮体，ω=3.14 rad/s；(b) 左侧浮体，ω=3.14 rad/s；
(c) 右侧浮体，ω=3.77 rad/s；(d) 左侧浮体，ω=3.77 rad/s；
(e) 右侧浮体，ω=4.40 rad/s；(f) 左侧浮体，ω=4.40 rad/s；
(g) 右侧浮体，ω=5.03 rad/s；(h) 左侧浮体，ω=5.03 rad/s

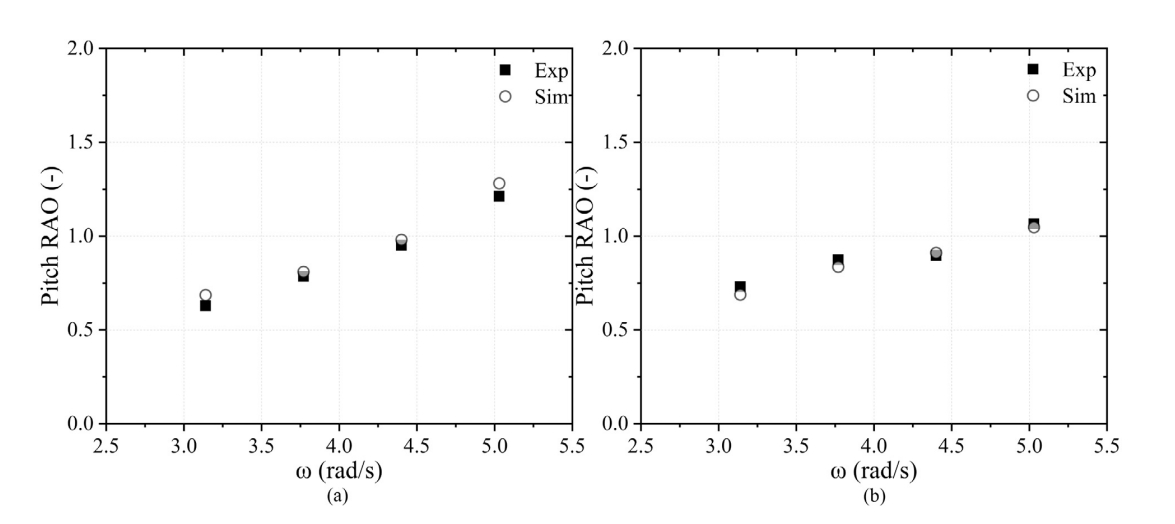
图9： 单铰接式波浪能转换器纵摇响应幅值算子（RAO）试验与数值结果对比：

(a) 右侧浮体；(b) 左侧浮体.

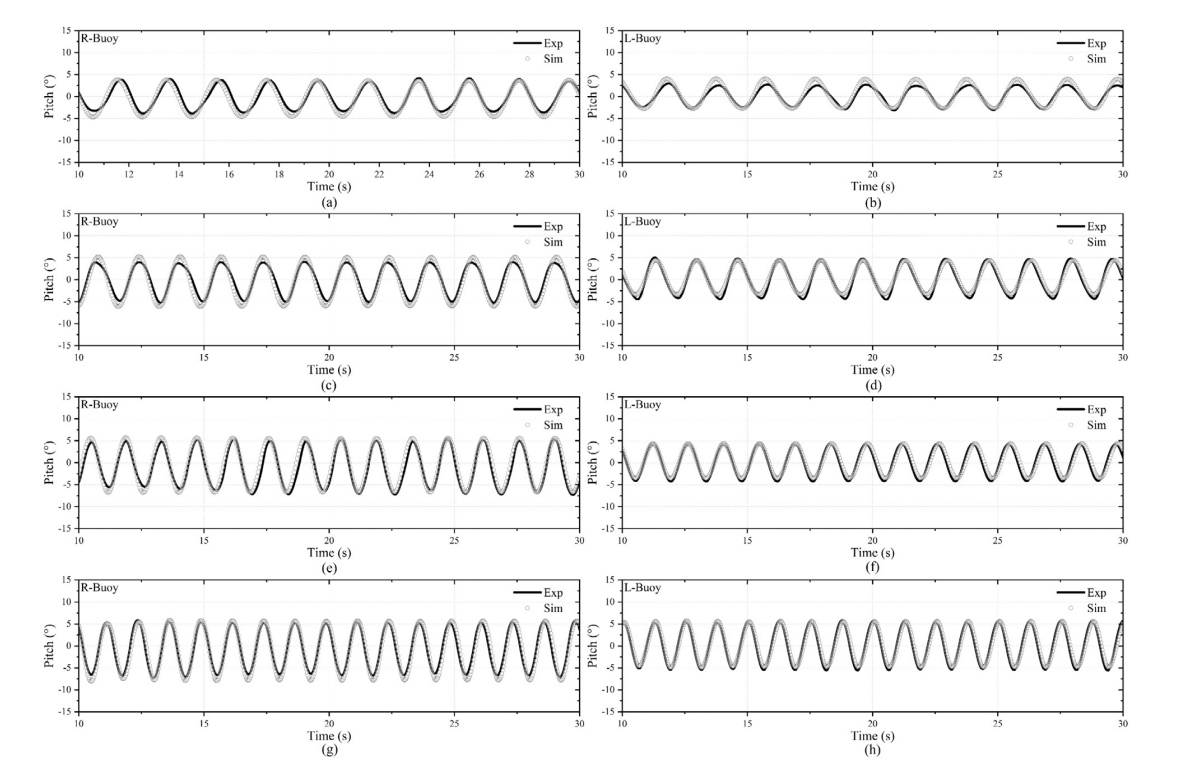
图10：双铰接式波浪能转换器数值模拟与试验结果对比验证（d/L=1/4）：

(a) 右侧浮体，ω=3.14 rad/s；(b) 左侧浮体，ω=3.14 rad/s；

(c) 右侧浮体，ω=3.77 rad/s；(d) 左侧浮体，ω=3.77 rad/s；

(e) 右侧浮体，ω=4.40 rad/s；(f) 左侧浮体，ω=4.40 rad/s；

(g) 右侧浮体，ω=5.03 rad/s；(h) 左侧浮体，ω=5.03 rad/s.

四、结果分析

本研究通过物理模型试验，系统探究了规则波况下浮体间距与波浪周期参数对单/双铰接双浮体波浪能转换装置（WEC）纵摇响应及系泊张力的影响规律。试验采用等效线性阻尼模型模拟动力输出（PTO）系统，并构建了对应的数值模型。数值计算结果与试验数据的高度吻合验证了模型的可靠性。基于验证模型开展的数值研究表明，铰接结构形式会显著影响双浮体系统的动力响应特性，研究进一步揭示了不同铰接类型对能量捕获效率的作用机制。

浮体间距优化：实验表明，单铰链WEC的最佳浮体间距比为1/3，双铰链WEC为1/4。双铰链配置在低频波浪条件下表现出更高的能量捕获效率。

PTO阻尼优化：研究发现，适度增加PTO阻尼可提高能量捕获效率，但过高的阻尼会降低浮体的运动幅度，影响整体性能。

波浪方向影响：双筏式WEC在顺波方向（波浪入射角为0°）时能量捕获效率最高，斜向波浪会降低能量捕获效率，但双铰链配置在不同波浪方向下均优于单铰链配置。

不规则波浪性能：在不规则波浪条件下，双铰链WEC的能量捕获效率显著优于单铰链配置，特别是在低频段表现出更强的捕获能力。

原文链接：

https://doi.org/10.1016/j.energy.2025.135611

参考文献：

Shi Wei, Yan Chaojun, Ren Zhengru, Yuan Zhiming, Liu Yingyi, Zheng Siming[1]et al. Review on the development of marine floating photovoltaic systems.Ocean Eng 2023;286(Part1):115560.

[2]Qiu Shouqiang, Liu Kum, Wang Dongjiao, Ye Jiawei, Liang Fulin. A compre-hensive review of ocean wave energy research and development in China.Renew Sustain Energy Rev 2019;113:109271.

[3] Falnes J. A review of wave-energy extraction. Mar Struct 2007;20:185-201

[4] Guo B, Ringwood JV. Geometric optimization of wave energy conversion devices:a survey. Appl Energy 2021;297:117100.

[5]Drew B, Plummer AR, Sahinkaya MN. A review of wave energy convertertechnology. Proc Inst Mech Eng Part A J Power Energy 2009;223:887-902.

[6] Wang L, Kolios A, Cui L, Sheng Q. Flexible multibody dynamics modelling ofpoint-absorber wave energy converters. Renew Energy 2018;127:790-801.

[7]Liu CH, Yang QJ,Bao G.Performance investigation of a two-raft-typewave energy converter with hydraulic power take-off unit. Appl Ocean Res2017:62:139-55.

[8]Czech B, Bauer P. Wave energy converter concepts: Design challenges andclassification. IEEE Ind Electron Mag 2012;6(2):4-16.

[9] Melikoglu M, Current status and future of ocean energy sources: A global review.Ocean Eng 2018;148:563-73.

[10]McCormick M, Murthagh J, McCabe P. Large-scale experimental study of ahinged-barge wave energy conversion system. In Proceedings of the 3rd europeanwave energy conference, Patras, Greece, 30 September-2 1998:215-222.

......................................................